formulate a linear programming model and solve using simplex method

Question

Relevant production data are as follows: Process, Time, Hours Product Cutting Sewing Material/Yard Skirt ½ 1 1 Dress 1 4 2 Suit 6 10 6 The SL makes skirts, dresses and suits. A new polyester knit fabric was introduced and SL decided to manufacture a line of their products with this material. They have devoted 100 hours of their cutting capacity and 120 hours of their sewing capacity per week to the new line. SL will buy only 70 square yards of the new material per week until the market demands for the new product line can be assessed. Each skirt sold nets $5 profit, each dress and suit sold nets $15 and $25 profit. SL wishes to maximize profits. Use simplex method to solve.

Answer 1

The objective is to maximise profit P. If x, y and z are the quantities of skirts, dresses and suits respectively then the objective is P=5x+15y+25z dollars, and the constraints are:

Cutting: x/2+y+6z≤100 hours

Sewing: x+4y+10z≤120 hours

Material: x+2y+6z≤70 sq yds

From this info an initial tableau can be constructed containing 3 slack variables s1, s2, s3 to be applied to the three constraint inequalities:

ROW	x	y	z	s1	s2	s3	P	Result	Ratio	Op/Comment
R1	0.5	1	6	1	0	0	0	100	16⅔	Cutting
R2	1	4	10	0	1	0	0	120	12	Sewing
R3	1	2	6	0	0	1	0	70	11⅔	Material
R4	-5	-15	-25	0	0	0	1	0		Objective

If this tableau is correct, the Simplex Method can be applied mechanically in progress stages. In this initial tableau, the pivot column (PC) is identified because the bottom row (R4) contains the most negative value. 

Ratio=Result/v, where v is the value in each row of PC corresponding to Result. That is, Ratio=100/6 for R1, 120/10 for R2, 70/6 for R3. The lowest ratio identifies the pivot row (PR) and the intersection of PC and PR identifies the pivot element (PE). This rule applies in some subsequent tableaux.

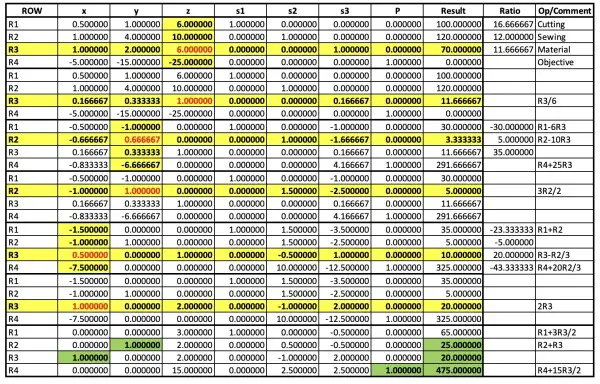
Each progressive tableau is shown as a group of 4 rows, with successive PEs shown in red within highlighted PC and PR. The initial tableau is also shown. All figures are to 6 decimal places.

Each row represents an equation, so that the variables, including the slack variables, sum to the result.

In the last tableau, s1=65hr so the first equation (R1), for example, is equivalent to:

x/2+y+z+s1=100=10+25+65=100 (x=20, y=25, z=0, s1=65, s2=s3=0, P=0).

Therefore x/2+y+z<100hr (35hr cutting, with 65hr to spare). The other constraints are at maximum (sewing=120hr, material=70 sq yds).

In particular, from R4 in the same tableau:

-5x-15y-25z+P=-100-375-0+475=0. Note that S2 and S3 as well as z are zero throughout.

In the final tableau skirts, x=20hr; dresses, y=25hr; and profit, P=$475, implying suits, z=0.

The required row operations are shown under Op/Comments.