Two observer p and q 32m apart on the same horizontal ground and the same side of a kite (k), observed the kite at angle of elevation 27° and 48° respectively, calculate correct to 1 decimal place

Question

(I) the height of the kite (II)the distance between the kiteand observer P

Answer 1

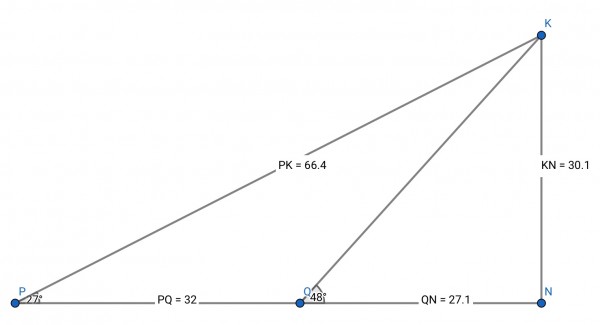
Let’s call h the height of the kite. And let x be the distance between observer Q and a position N on the ground directly beneath the kite (that is, a distance h below the kite).

We can write two equations based on the tangents of the two angles. The distance of observer P from N is 32+x. We have two triangles: PKN and QKN, where KN=h, QN=x, PN=32+x.

tan(48)=h/x and tan(27)=h/(32+x). Therefore h=xtan(48), so tan(27)=xtan(48)/(32+x), (32+x)tan(27)=xtan(48), 32tan(27)+xtan(27)=xtan(48), x(tan(48)-tan(27))=32tan(27), and x=32tan(27)/(tan(48)-tan(27))=27.1m to 1 decimal place.

(i) h=xtan(48)=30.1m

(ii) sin(27)=KN/PK=h/PK, so PK, the distance between the kite and observer P=h/sin(27)=66.4m.