Linear Programming help

Question

Avineyard produces two special wines, a white and a red. A bottle of the white wine requires 14 pounds of grapes and 1 hour of processing time. A bottle of red wine requires 25 pounds of grapes and 2 hours of processing time. The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing time to the production of these wines. A bottle of the white wine sells for $11.00, while a bottle of the red wine sells for $25.00. How many bottles of each type should the vineyard produce in order to maximize gross sales?

 

Answer 1

Let’s use W and R for the number of bottles of white and red wine. The objective function is P=25R+11W, and $P must be a maximum profit.

The constraints are that R and W are both positive whole numbers and:

Grapes: 25R+14W≤2198

Processing time: 2R+W≤160

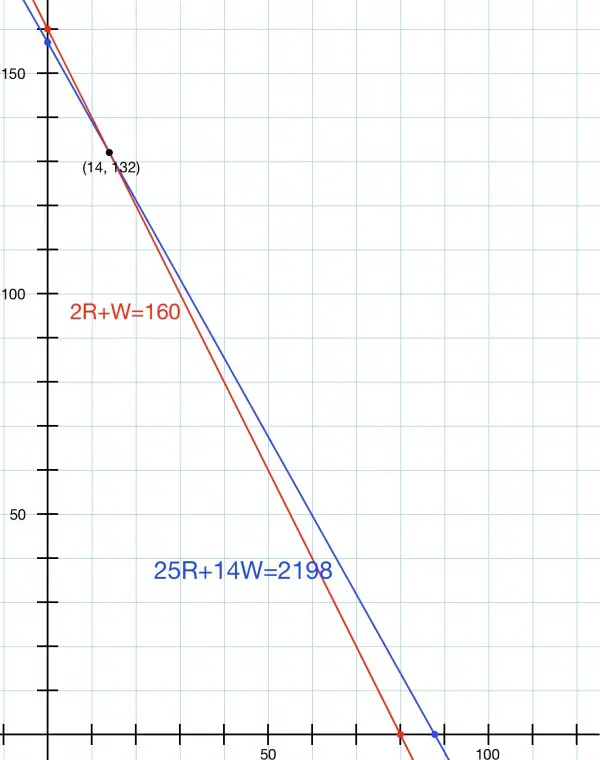
The feasible region is below both lines and enclosed by the axes. The vertical axis is white wine quantity and the horizontal axis is the red wine quantity.

The lines intersect at the solution of 25R+14W=2198 and 2R+W=160. W=160-2R so we can substitute in the first equation: 25R+2240-28R=2198. 3R=42, R=14 and W=132.

We can ignore zero profit at (0,0). There are three other vertices to consider: (0,157), (14,132) and (80,0).

The value of P for each is respectively: $1727, $1802, $2000. So the maximum profit of $2000 is 80 bottles of red wine and no white wine.