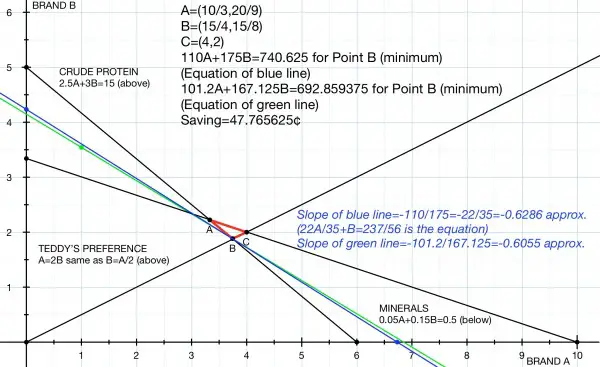
The graph above shows a feasibility area, the red triangle ABC when the constraints are applied. The blue and green lines show the objective expression which has to be minimised. The blue line is the equation of the objective function before discounts are applied to the costs, and the green line the equation after discounts.
The blue and green lines pass through vertex B of the feasibility triangle. A detailed explanation and solution follow below.
Let A=number of cups of Brand A and B=number of cups of Brand B. The cost forms the objective function F=110A+175B and we need the minimum value of F.
The constraints are based on the quantities of crude protein and minerals.
Teddy’s preference can be expressed as A≤2B, meaning that the quantity of Brand A is at most twice that of Brand B.This inequality can also be written B≥A/2. For example, if there’s one cup of B then Teddy prefers no more than 2 cups of A, or if there are 2 cups of A then there’s at least one cup of B. With B as the vertical axis we draw the graph B=A/2, and the open area above and on the line represents B≥A/2.
The next constraint is the amount of crude protein. Teddy needs at least 15g so since we know that Brand A contains 2.5g per cup and Brand B 3g per cup: 2.5A+3B≥15 the total crude protein content in grams.
Finally, there must be no more than 0.5g of minerals so 0.05A+0.15B≤0.5 is the total mineral content in grams.
The area above the crude protein line and the area below the mineral line represent the constraints.
Combining these constraints graphically we can see that the red triangle ABC is the feasible region.
Now we need to work out the coordinates of A, B and C. We do this by solving systems of simultaneous equations.
Vertex A is at the intersection of 2.5A+3B=15 and 0.05A+0.15B=0.5:
Multiply the second equation by 20: A+3B=10, which when subtracted from the first equation gives 1.5A=5, making A=10/3. So we can find B=⅓(10-A)=20/9. A is (10/3,20/9) and F=6800/9=755.56 approx.
Vertex B is at the intersection of 2.5A+3B=15 and B=A/2:
Substitute for B: 2.5A+1.5A=15, 4A=15, A=15/4 and B=15/8. B is (15/4,15/8) and F=5925/8=740.625.
Vertex C is at the intersection of B=A/2 and 0.05A+0.15B=0.5:
Substitute for B: 0.05A+0.075A=0.5, 0.125A=0.5, A=4 and B=2. C is (4,2) and F=790.
The minimum value for F=740.625 is at vertex B(15/4,15/8).
The cost can be represented by the blue line. The slope of this line is -110/175 where negative implies a line sloping backwards. Graphically we are looking at 110A+175B=F which, until F is defined, is a set of parallel lines. We need the line that is as far over to the left as possible but within the red triangle. Vertex B is a point on the blue line, because the slope of the objective line is between the slopes of the crude protein and mineral lines. The equation is 110A+175B=740.625. At this point Teddy gets his preference, the crude protein content is 15g and the mineral content is 0.05A+0.15B=15/32g=0.46875, which lies below the mineral line, meeting the constraint that the content is no more than 0.5g.
The costs change when discount is applied, but the constraints remain the same.
The new objective function is 0.92×110A+0.955×175B=F, that is, 101.2A+167.125B=F. The green line shows the discounted function. Point B is still the required point and F=44343/64=692.859375.
Thus, Mr Bean makes a saving of 740.625-692.859375=3057/64=47.765625 cents.
In each case he should use 15/4 cups (3.75) cups of Brand A and 15/8 cups (1.875) cups of Brand B.